Theoretical Condensed Matter Physics
Current projects
Doped kagome antiferromagnet
In 1973 Anderson proposed a new kind of insulating phase as an alternative to the magnetically long-range ordered (Néel) phase for the ground state of two-dimensional frustrated
antiferromagnets. In this phase, the magnetic moments are highly correlated and yet fluctuate strongly down to zero temperature. This strong correlation comes about because the spins,
owing to the antiferromagnetic interaction, pair up into valence-bonds (configurations with zero total spin) which are able to move around freely between pairs of atoms. The resulting
fluid-like state of matter is known as a spin-liquid in the literature.
Spin liquids avoid any spontaneous symmetry breaking at any temperature. Naturally the existence of so exotic a phase is counter intuitive since our everyday day experience tells us that
cold matter exhibits broken symmetries. Hence, the study of models displaying spin-liquid behavior is rather interesting.
Nowadays there is a general agreement that the ground state of the Heisenberg model on the kagomé lattice is a spin-liquid, yet no conclusion has been reached regarding its specific
nature. For this reason it is interesting to consider perturbations to the ground state of the Heisenberg model.
We are interested in the hole-doped version of the kagomé Heisenberg antiferromagnet (the so-called t-J model). We seek to understand the effect of a few propagating holes on the magnetic
properties of a system of strongly correlated spins using mean-field theory and variational Monte Carlo methods.
Modular forms and functions
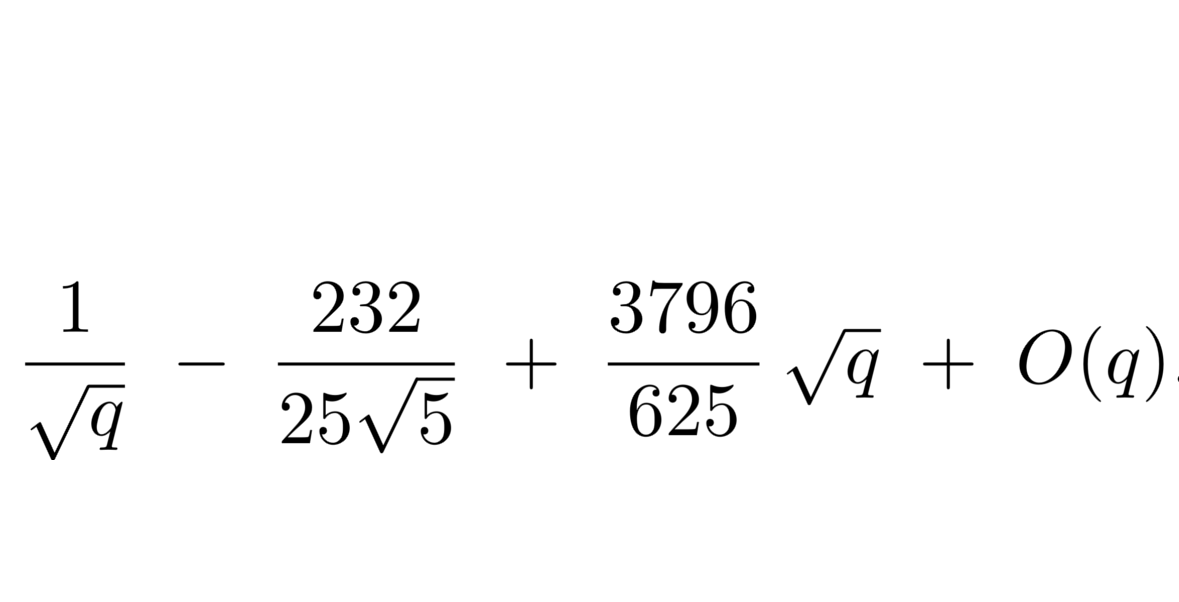 Modular forms play an important role in number theory, algebraic
geometry and physics. We are interested in finding methods of calculating them - especially in the case of non congruence subgroups of the modular group.
Modular forms play an important role in number theory, algebraic
geometry and physics. We are interested in finding methods of calculating them - especially in the case of non congruence subgroups of the modular group.
Dessin d'enfants
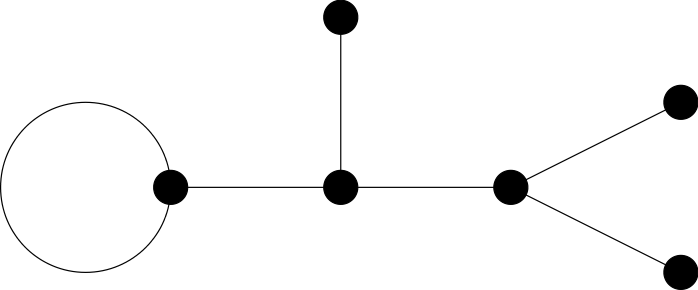 We are interested in the relation between Dessin, finite-index subgroups of the modular
group and Belyi-function. Especially we would like to find the Belyi-function from a given Dessin.
We are interested in the relation between Dessin, finite-index subgroups of the modular
group and Belyi-function. Especially we would like to find the Belyi-function from a given Dessin.
Farey Symbols
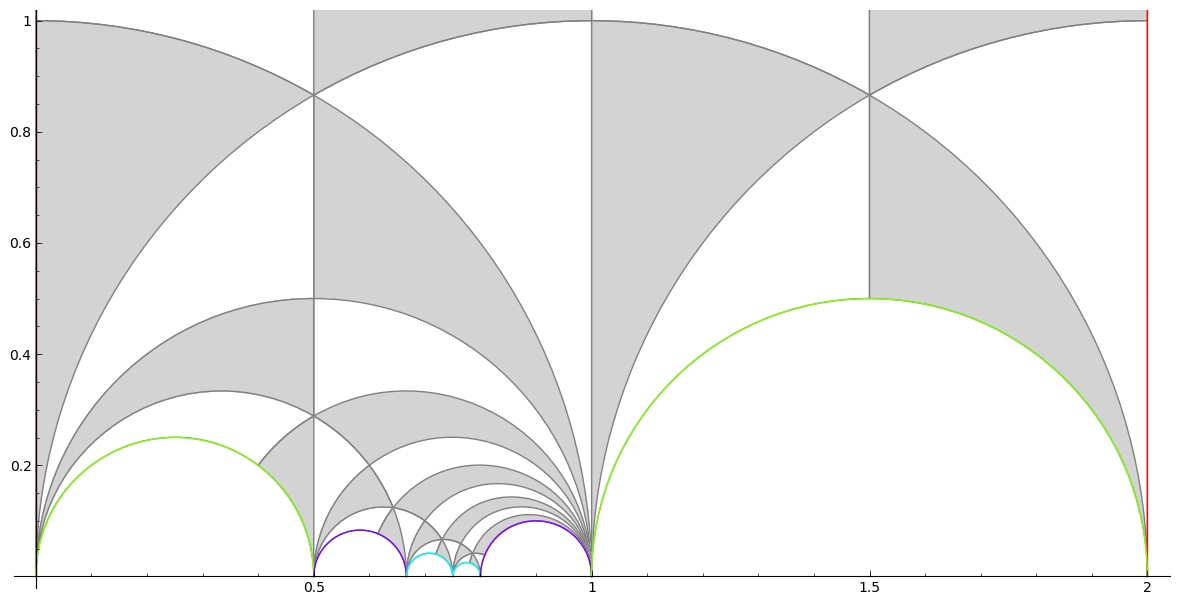 A powerful tool for studying the modular group and its finite index subgroups was
introduced by Ravi S. Kulkarni in 1991: "An arithmetic-geometric method in the study of the subgroups of the modular group", Amer. J. Math.,
113(6):1053-1133, 1991.
A powerful tool for studying the modular group and its finite index subgroups was
introduced by Ravi S. Kulkarni in 1991: "An arithmetic-geometric method in the study of the subgroups of the modular group", Amer. J. Math.,
113(6):1053-1133, 1991.
We provided a complete and efficient implementation for the computer algebra system sage
 Farey Symbols in
SAGE
Farey Symbols in
SAGEPhenomenological theory of the 3 K phase in Sr2RuO4
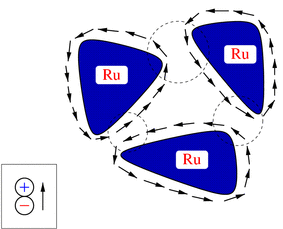
 J. Phys. Soc. Jpn. 70,2409 (2001)
J. Phys. Soc. Jpn. 70,2409 (2001)
Charge ordering and spin-Peierls phenomena in NaV2O5
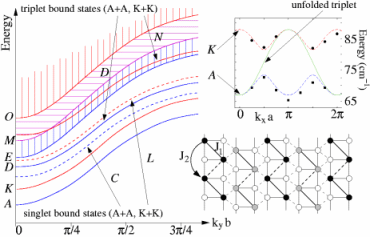
 Phys. Rev. B 62, R14613 (2000)
Phys. Rev. B 62, R14613 (2000)
Cluster Expansions for Two-Particle Bound States
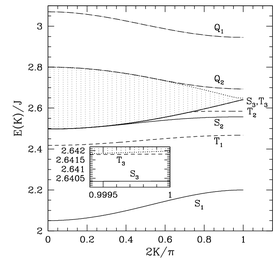
 Phys. Rev. B 63, 144410 (2001)
Phys. Rev. B 63, 144410 (2001)
Phys. Rev. B 63, 144411 (2001)
Phys. Rev. Lett. 85, 4373 (2000)
Nonequilibrium DMFT
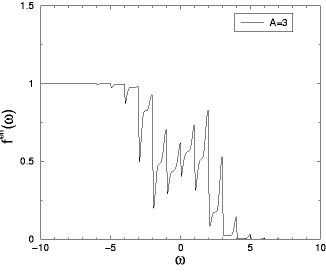
 http://arxiv.org/abs/cond-mat/0202046
http://arxiv.org/abs/cond-mat/0202046
Charge density wave systems
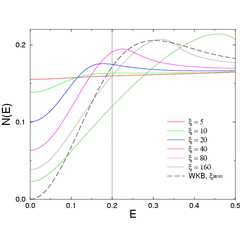
 Phys. Rev. Lett. 87, 126402, (2001)
Phys. Rev. Lett. 87, 126402, (2001)
Phys. Rev. B 61, 12496 (2000)
Phys. Rev. Lett. 84, 2546 (2000)
Phase transitions in the Bose-Hubbard model
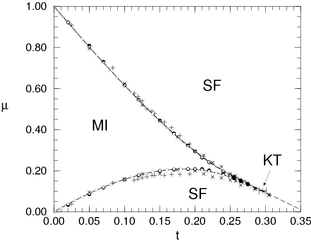
 Phys. Rev. B 61, 12474 (2000)
Phys. Rev. B 61, 12474 (2000)
Phys. Rev. B 60, 2357 (1999)
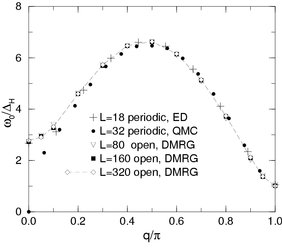
Dynamics with DMRG
Pseudogaps in high-Tc

 What is wrong with paramagnons? (Preprint)
What is wrong with paramagnons? (Preprint)